AP Calculus AB Differential Equations delves into the fascinating realm of differential equations, equipping students with the analytical tools to unravel complex phenomena in diverse scientific disciplines.
This comprehensive guide will navigate the intricacies of solving differential equations, exploring their applications in real-world scenarios, and empowering students to construct mathematical models that capture the essence of physical processes.
Definition of Differential Equations
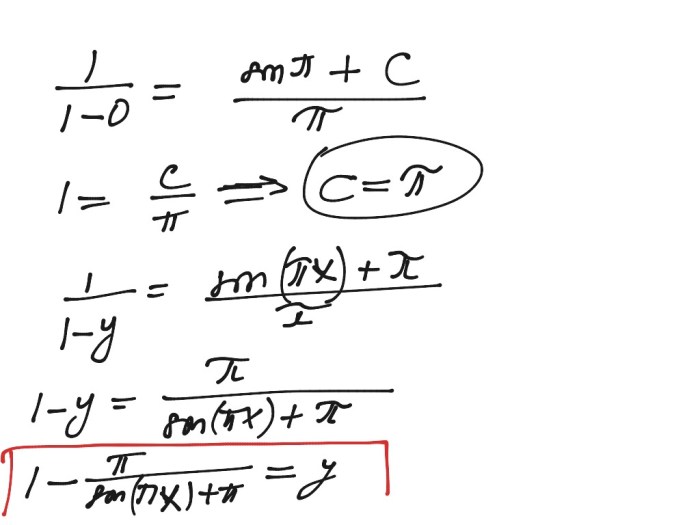
In mathematics, a differential equation is an equation that involves an unknown function and its derivatives. Differential equations are used to model a wide variety of phenomena in the natural world, including population growth, the motion of objects, and the flow of fluids.
In AP Calculus AB, we will focus on first-order differential equations, which are equations that involve the first derivative of the unknown function. First-order differential equations can be used to model a variety of phenomena, including:
- The growth of a population
- The motion of an object in a straight line
- The flow of water in a pipe
Solving First-Order Differential Equations
There are a variety of methods for solving first-order differential equations. One common method is the method of separation of variables. This method involves rewriting the differential equation in a form that can be separated into two equations, one involving the unknown function and the other involving the independent variable.
The two equations can then be solved separately to find the unknown function.
Another common method for solving first-order differential equations is the method of integrating factors. This method involves multiplying the differential equation by a function called an integrating factor. The integrating factor is chosen so that the resulting equation can be integrated to find the unknown function.
Solving Differential Equations

Differential equations are mathematical equations that involve the derivatives of a function. Solving differential equations is an important technique in mathematics and science, as it allows us to understand how systems change over time.
Methods for Solving First-Order Differential Equations
There are several methods for solving first-order differential equations, including:
- Separation of variables
- Integrating factors
Separation of Variables
The separation of variables method involves separating the equation into two equations, one involving only the dependent variable and the other involving only the independent variable. This method is useful when the equation can be written in the form:
“`y’ = f(x)g(y)“`
To solve using separation of variables, we integrate both sides of the equation with respect to x and y:
“`∫y’ dx = ∫f(x)g(y) dy“`
This gives us two equations:
“`y = ∫g(y) dy + C₁“““x = ∫f(x) dx + C₂“`
where C₁ and C₂ are constants of integration.
Integrating Factors
The integrating factors method involves multiplying the equation by a function called an integrating factor, which makes the equation easier to solve. The integrating factor is given by:
“`μ(x) = e^(∫p(x) dx)“`
where p(x) is the coefficient of the y’ term in the equation.
To solve using integrating factors, we multiply the equation by the integrating factor and then integrate both sides of the equation with respect to x:
“`μ(x)y’ + μ(x)p(x)y = μ(x)f(x)“““∫(μ(x)y’ + μ(x)p(x)y) dx = ∫μ(x)f(x) dx“`
This gives us the solution:
“`y = e^(-∫p(x) dx) (∫μ(x)f(x) dx + C)“`
where C is a constant of integration.
Comparison of Methods
The following table compares the separation of variables and integrating factors methods for solving first-order differential equations:
| Method | Advantages | Disadvantages |
|---|---|---|
| Separation of variables | Easy to use | Not always applicable |
| Integrating factors | More general | More difficult to use |
Applications of Differential Equations: Ap Calculus Ab Differential Equations
Differential equations play a pivotal role in modeling and analyzing various physical phenomena across diverse scientific disciplines. They provide a powerful tool to describe and predict the behavior of dynamic systems over time.
Physics
- Motion and Dynamics:Differential equations govern the motion of objects under the influence of forces, such as projectiles, pendulums, and celestial bodies. They enable scientists to calculate trajectories, velocities, and accelerations.
- Fluid Dynamics:Differential equations model the flow of fluids, including water, air, and blood. They are used to design aircraft wings, optimize pipelines, and study weather patterns.
- Thermodynamics:Differential equations describe the transfer of heat and energy in systems. They are essential for understanding heat engines, refrigerators, and climate modeling.
Chemistry
- Chemical Reactions:Differential equations model the rates of chemical reactions and predict the concentrations of reactants and products over time. They are used in the design of chemical processes and drug development.
- Diffusion and Mass Transfer:Differential equations describe the movement of molecules and particles through space. They are used to study processes such as diffusion, osmosis, and filtration.
Biology
- Population Dynamics:Differential equations model the growth and decline of populations, taking into account factors such as birth rates, death rates, and environmental carrying capacity.
- Epidemiology:Differential equations are used to track the spread of infectious diseases and predict the effectiveness of vaccination programs.
- Physiology:Differential equations describe the electrical activity of neurons, the flow of blood through the circulatory system, and the dynamics of biological control systems.
Modeling with Differential Equations
Differential equations play a crucial role in modeling real-world problems by translating them into mathematical equations. This allows us to analyze, predict, and make informed decisions based on the underlying dynamics of the system being studied.
To effectively model with differential equations, it is essential to identify the following key elements:
Variables
- Dependent variables:Represent the quantities whose values change over time.
- Independent variables:Represent the variables that affect the dependent variables.
Parameters
Constants that describe the specific characteristics of the system being modeled.
Initial Conditions
The values of the dependent variables at a specific time or point.
Step-by-Step Process for Modeling with Differential Equations
- Identify the variables, parameters, and initial conditions.Determine the quantities that change over time, the factors that affect them, and the known values at a specific point.
- Formulate the differential equation.Based on the relationship between the variables and parameters, write down the equation that describes the rate of change of the dependent variables.
- Solve the differential equation.Use appropriate mathematical techniques to find the function that represents the solution to the equation.
- Apply the initial conditions.Substitute the known values into the solution to determine the specific function that describes the system’s behavior.
- Analyze the solution.Interpret the solution to understand the behavior of the system, make predictions, and draw conclusions.
Graphical Analysis of Differential Equations
Graphical analysis of differential equations involves techniques for sketching solution curves, which provide a visual representation of the behavior of solutions. These curves help identify the types of solutions and their characteristics, such as stability, direction of motion, and equilibrium points.
Sketching Solution Curves
To sketch solution curves, we can use the slope field method. In this method, we calculate the slope of the solution at each point in the domain and draw short line segments with the corresponding slopes. The solution curve is then drawn as a smooth curve tangent to these line segments.
Types of Solution Curves, Ap calculus ab differential equations
The types of solution curves include:
-
-*Stable Equilibrium
A point where the solution curve approaches and remains at after a small perturbation.
-*Unstable Equilibrium
A point where the solution curve moves away from after a small perturbation.
-*Saddle Point
A point where the solution curve approaches from one direction and moves away in another direction.
-*Limit Cycle
A closed curve that the solution curve approaches and remains on after a long time.
Applications
Graphical analysis of differential equations has applications in various fields, such as:
- Population growth and decay
- Chemical reactions
- Heat transfer
- Electrical circuits
- Mechanical systems
Frequently Asked Questions
What are differential equations?
Differential equations are mathematical equations that involve derivatives of unknown functions. They describe the relationship between the rate of change of a function and its value.
How are differential equations used in real-world applications?
Differential equations are used to model a wide range of phenomena, including population growth, radioactive decay, fluid flow, and the motion of celestial bodies.
What are the different methods for solving differential equations?
There are various methods for solving differential equations, including separation of variables, integrating factors, and Laplace transforms.